1 前言
隨著科技的發展，人們生活水平的提高，對“質量”將會更加的關注，特別是關于國計民生工程。眾所周知，在制造行業中，要想獲得百分百的質量肯定，最可靠的辦法是百分百檢驗，而百分百的檢驗會給質量檢驗機構增加無盡的負擔，給生產帶來無限期的延遲。本文闡述的是，在鋁材制造過程中常見的問題分析方法。鋁材的硬度是否和抗拉強度存在一定的線性？是否能建立回歸方程輔助車間質量檢測員方便快捷的判別產品是否合格？這樣的線性與回歸是不是能在生產過程中得以驗證？我們帶著這些問題以6061-T6鋁板為例，一起去探究。現將項目內容簡介如下：
2 試驗部分
2.1 試驗準備
2.1.1 在擠壓車間日常生產的6061-T6鋁板中隨機抽取25天試驗樣本，鋁板中含有1-7mm不同厚度。
2.1.2 硬度試驗參照YS/T 420-2000方法操作，抗拉強度采用萬能微機控制電子萬能試驗儀測量，試驗方法按GB/T 228-2002中規定進行。
2.2 試驗操作
2.2.1 硬度測試試驗
2.2.1.1 試樣的厚度為1-7mm，試樣的表面應光滑，潔凈，不應有機械損傷，試樣邊緣不應有毛刺，如試驗有輕微的擦劃應輕輕的磨光，試樣的最小尺寸約為25mm×25mm，并保證測量時壓痕到邊緣的距離不小于3mm。
2.2.1.2 將試驗置于砧座和壓針之間，壓針應與試驗面垂直，輕輕壓下手柄，使壓針壓住試樣。快速的壓下手柄，施加足夠的力，使壓針套筒的斷面緊壓在試樣上，在表頭讀出硬度值。每個試驗測量5點，以算術平均值作為試樣的硬度值，并且記錄。
2.2.2 力學性能試驗
2.2.2.1 本次力學性能測試試樣采用GB/T 228-2002 中規定的P5試樣(矩形橫截面非比例試樣)。
2.2.2.2 將試樣置于萬能材料試驗機的夾具中，運行儀器，以10mm/min的速度進行拉伸試驗，通過電腦自動將所加載的載荷和相應位移記錄下來，直到最大載荷的出現。試樣完成后，將抗拉強度值記錄下來。
2.3 試驗結果
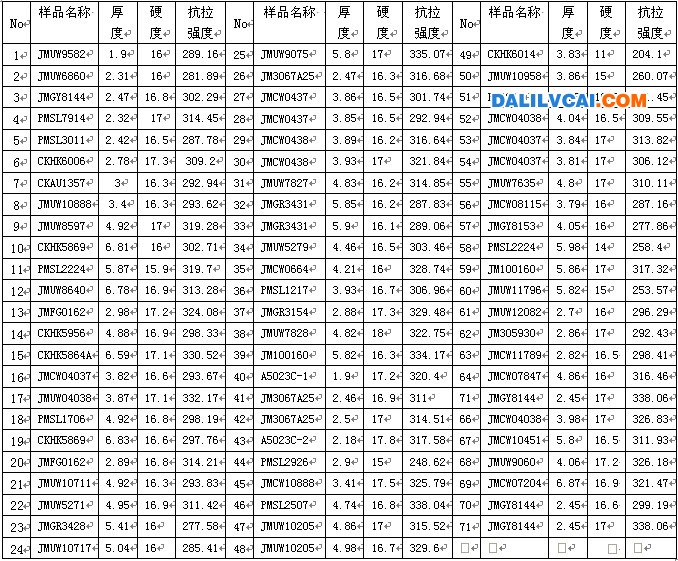
本次試驗我們針對不同厚度的6061-T6鋁板進行了抗拉強度，硬度測試，試驗結果如下：
2.4.1 相關分析
相關系數r(通常是指Pearson相關系數)，是用來描述兩個變量線性相關程度的一種度量。若x與y無關時，相關系數r應該為0。一般來說，樣本量超過9時，只要相關系數的絕對值達到0.7，那么認為兩變量間確實相關的，當樣本量超過25時，只要相關系數絕對值達到0.4，那么就應當認定兩變量確實是相關的。
2.4.1.1 由于樣本較大，我們采用計算機輔助計算。用MINITAB軟件從STAT-Basic Statistics-Correlation入口，直接得到下面結果：
相關: 硬度, 抗拉強度
硬度和抗拉強度的Pearson相關系數 = 0.806
P值 = 0.000
2.4.1.2 因為相關系數為0.806，由此確定硬度與抗拉強度確實存在著線性關系。從樣本中看出，所取的樣本是從1-7mm的鋁板，如果把樣本分為兩組1-3mm、3-7mm分別分析它們的相關系數：
相關(0-3mm): 硬度, 抗拉強度
硬度和抗拉強度的Pearson相關系數 = 0.823
P值 = 0.000
相關(3～7mm): 硬度, 抗拉強度
硬度 和 抗拉強度 的 Pearson 相關系數 = 0.824
P值 = 0.000
2.4.1.2 從上述分析中看出，把樣本分組得到的相關系數r要大，說明分組后線性相關越強，后續分析的一元線性回歸模型將作分組分析。
2.4.2 一元線性回歸模型
假定(x，y)的散點圖顯示有線性關系，則可以認為觀測值由兩部分迭加而成：一是y的平均值隨x的變化而呈線性關變化的趨勢，用b0+b1x表示；而是其他隨機因素影響到y值本身會偏離平均值，其誤差用ε表示，常設ε~N（0，σ2），固有如有的數據結構式：yi=b0+b1xi+εi，i=1,2，...n，用求導函數的方法得回歸系數的最小二乘估計：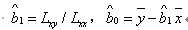
，
2.4.2.1 建立回歸方程(利用MINITAB應用軟件，由STAT-Regresstion-FittdLine-Plot入口)
2.4.2.1.1 1～3mm鋁板的回歸方程分析
回歸分析(1～3mm): 抗拉強度 與 硬度
回歸方程為
抗拉強度 = - 130 + 26.0 硬度
系數標
自變量 系數 準誤 T P
常量 -129.84 65.66 -1.98 0.061
硬度 26.045 3.926 6.63 0.000
S = 11.0001 R-Sq = 67.7% R-Sq（調整） = 66.2%
2.4.2.2 3～7mm鋁板的回歸方程分析
回歸分析(3-7mm): 抗拉強度 與 硬度
回歸方程為
抗拉強度 = - 21.5 + 19.9 硬度
系數標
自變量 系數 準誤 T P
常量 -21.50 32.77 -0.66 0.515
硬度 19.936 1.996 9.99 0.000
S = 14.2201 R-Sq = 68.0% R-Sq（調整） = 67.3%
2.4.3 回歸方程的顯著性檢驗
我們建立回歸方程的目的是去表達兩個具有線性相關的變量間的定量關系，因此，只有當兩個變量確實具有線性相關關系時建立的回歸方程才是有意義的。兩變量間是否存在線性相關關系，有兩種檢驗方法：一是上述已經分析的相關系數法，而另外一種是方差分析法。
2.4.3.1 1～3mm鋁板的回歸方程顯著性檢驗
方差分析
來源 自由度 SS MS F P
回歸 1 5325.1 5325.1 44.01 0.000
殘差誤差 21 2541.0 121.0
合計 22 7866.1
經過分析p-value值為0.000,比0.001還小，故認為回歸方程是有意義的。
2.4.3.2 3～7mm鋁板的回歸方程顯著性檢驗
方差分析
來源 自由度 SS MS F P
回歸 1 20176 20176 99.78 0.000
殘差誤差 47 9504 202
合計 48 29680
經過分析p-value值為0.000,比0.001還小，故認為回歸方程是有意義的。
2.4.4 利用回歸方程作預測
當求得一個有意義的回歸方程后，可以將此回歸方程進行預測。如果給定x的值為x0，那么y的預測值為：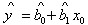
,y的概率為1-a的預測區間：
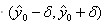, σ的精確表達式：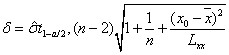
(利用MINITAB應用軟件: STAT-Regresstion-FittdLine-Plot入口)
2.4.4.1 1～3mm鋁板的回歸方程的預測區間：(由于數據較多，先只列出幾個抗拉強度值的預測區間)
新觀測值的預測值
新觀 擬合值
測值 擬合值 標準誤 95% 置信區間 95% 預測區間
1 286.88 3.62 (279.35, 294.42) (262.80, 310.97)
3 307.72 2.32 (302.90, 312.54) (284.34, 331.10)
5 299.91 2.44 (294.83, 304.99) (276.47, 323.34)
2.4.4.1 3～7mm鋁板的回歸方程的預測區間：(由于數據較多，先只列出幾個抗拉強度值的預測區間)
新觀測值的預測值
新觀 擬合值
測值 擬合值 標準誤 95% 置信區間 95% 預測區間
1 303.46 2.04 (299.36, 307.56) (274.56, 332.36)
2 317.42 2.37 (312.65, 322.19) (288.41, 346.42)
3 297.48 2.17 (293.11, 301.85) (268.54, 326.42)
2.4.5 殘差分析：證實模型假定
使用回歸方程的上述統計檢驗可以獲得有關X和Y的豐富信息，但仍然不能確定設定的回顧模型是否與數據擬合得很好。為了確認擬合效果，必須采用殘差分析方法來進行診斷。定義在 處的殘差 是因變量的觀測值( )與因變量的估計值 之差，即： = — ，換言之， 處的殘差是利用估計的回歸方程去預測 而引起的誤差。
2.4.5.1 1～3mm鋁板的回歸方程的殘差分析（見下表）
2.4.5.1.1 殘差圖的正態性檢驗。從下圖（圖1左上圖）可以看出，10個樣本點呈直線狀，沒有發現任何不正常之處。
2.4.5.1.2 關于因變量的預測值的殘差圖（圖1右上圖）。這種殘差圖是在水平軸上表示因變量的預測值和在縱軸上表示殘差值。如果在圖中有明顯的“喇叭口”形狀，即表明殘差的標準差不是常數，而是在隨預測值的變化。在本圖中沒有發現任何不正常之處。
2.4.5.1.3 關于按觀測順序的殘差圖（圖1右下圖）。關于按觀測順序的殘差圖是用水平軸表示觀測順序，用縱軸表示對應的殘差值。這些殘差點應在橫軸（即殘差為0）上下隨機波動，不應有任何上升，下降，擺動，跳躍等趨勢。如果有某種趨勢存在，則說明數據觀測過程中受到某個某個未知的因素的強大的影響，應該找出此因素并加以控制。在本圖中沒有發現任何不正常之處。
2.4.5.1.4 關于自變量X的值的殘差圖（圖2）。在分析過程中此圖沒有任何不正常之處。
2.4.5.1.5 殘差圖并沒有提供足夠的證據，使我們對回歸模型所的假定表示懷疑。這將導致我們在最后能夠確信，[抗拉強度 = - 130 + 26.0 硬度]簡單線性回歸模型是合理的。
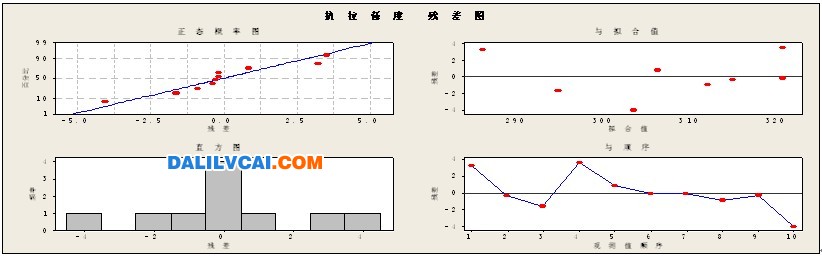
圖1
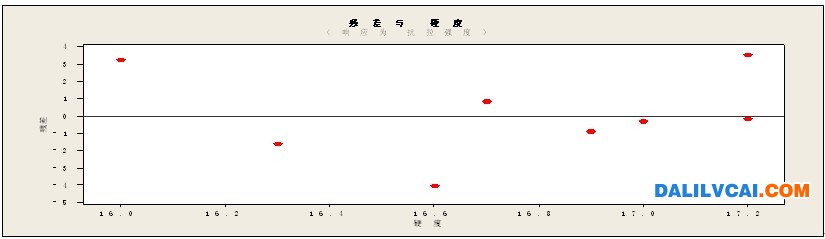
圖2
2.4.5.2 3～7mm鋁板的回歸方程的殘差分析。按照2.4.5.1.1-2.4.5.1.4的步驟分析，確定[抗拉強度 = - 21.5 + 19.9 硬度] 簡單線性回歸模型是合理的。
3 結論
3.1 此次試驗簡述怎么運用了線性分析與回歸分析方法對生產過程中的自變量與因變量進行分析，通過回歸方程預測，初步確定產品的質量水平，建議廣大讀者在生產過程中大力推廣。
3.2 本文得出的回歸方程為：
3.2.1 1～3mm鋁板抗拉強度與硬度的回歸方程：Rm = - 130 + 26.0×Hw,其中Rm為抗拉強度，Hw為硬度。
3.2.2 3～7mm鋁板抗拉強度與硬度的回歸方程：Rm = - 21.5 + 19.9×Hw，其中Rm為抗拉強度，Hw為硬度。
3.3 本文得出的方程只能為本企業內部使用控制，如果在更換原材料，改變6061合金成份以及改變生產工藝等條件下，必須重新再做分析，以前的結論作廢。
